Linux Journal has an article in the January 2005 issue that introduces a doubly linked list that is designed for memory efficiency.

Typically elements in doubly linked list implementations consist of a pointer to the data, a pointer to the next node and a pointer to the previous node in the list.

The more memory efficient implementation described in the article stores a single offset instead of the next and previous pointers.

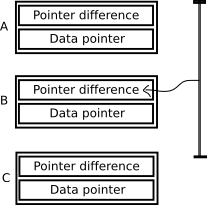
The pointer difference is calculated by taking the exclusive or (XOR) of the memory location of the previous and the next nodes. Like most linked list implementations a NULL pointer indicates a non-existent node. This is used at the beginning and end of the list. For the diagram above, the pointer differences would be calculated as follows:

A[Pointer difference] = NULL XOR B
B[Pointer difference] = A XOR C
C[Pointer difference] = B XOR NULL

One nice property of XOR is that it doesn’t matter what order the operation is applied. For example:
A XOR B = C
C XOR B = A
A XOR C = B

The memory efficient linked list uses this property of XOR for traversals. The trick is that any traversal operation requires both the address of current node and the address of either the preceding or following node.

Using the example figure above, calculating the address of the B node from A looks like:
B = NULL XOR A[Pointer difference]

What is really interesting is that traversing the list operates exactly the same in both directions. As shown below calculating the address of node A or C from B is simply depends on which direction the traversal is going.

A = C XOR B[Pointer difference]
C = A XOR B[Pointer difference]

The original article presents some time and space complexity results. I won’t bother repeating them here.

I am finally getting caught up on some magazine reading that I fell behind on during the school year. Today, I was reading a article called Parallel Universes by Max Tegmark in the May 2003 issue of Scientific American. I am not a physicist so some of this article is over my head but most of it was quite understandable. Reading that there are plausible arguments as to why parallel universes might exist was quite a surprise.

I found a couple of choice quotes that I think are worth sharing:

“But an entire ensemble is often much simpler than one of it’s members. This principle can be stated more formally using the notion of algorithmic information content. The algorithmic information content in a number is, roughly speaking, the length of the shortest computer program that will produce that number as output. For example, consider the set of all integers. Which is simpler, the whole set or just one number? Naively, you might think that a single number is simpler, but the entire set can be generated by quite a trivial computer program, whereas a single number can be hugely long. Therefore, the whole set is actually simpler.”

“The lesson is that complexity increases when we restrict out attention to one particular element in an ensemble, thereby losing the symmetry and simplicity that were inherent in the totality of all the elements taken together.”

These quotes jumped out at me because they touch on what I think is perhaps the most basic aspect of Computer Science and programming, finding the hidden simplicity. Often, there is a gorgeous, simple solution to the problem. It just takes time to get the complexity out of the way.

SlashDot recently posted an article about LOAF. LOAF is an interesting idea. The site is worth looking at for it’s own sake. However, what I found really interesting was the tidbit of computer science behind LOAF called a Bloom Filter.

A Bloom Filter uses multiple hash functions and a large bit array to represent a set. The set cannot be reconstructed from the Bloom Filter. There is a small possibility that the Bloom Filter will return a false positive but a false negative is impossible.

Here are some links with more information:

• Bloom Filters – the math
• A little Bloom Filter Theory
• Network Applications of Bloom Filters: A Survey
• perl.com: Using Bloom Filters

The original article on Bloom filters:

Communications of the ACM
Volume 13 , Issue 7 (July 1970)
Pages: 422 – 426
Year of Publication: 1970
ISSN:0001-0782

This article is available in the ACM digital library.